• Generate Aes 256 Key Python 3.5
• Generate Aes 256 Key Python 3.7
• Generate Aes 256 Key Python
• Generate Aes 256 Key Python 3

Warning

Please do not mistake this article for anything more than what it is: myfeeble attempt at learning how to use PyCrypto. If you need to useencryption in your project, do not rely on this code. It is bad. It willhaunt you. And some cute creature somewhere will surely die a painfuldeath. Don't let that happen.

Encryption Key Generator. The all-in-one ultimate online toolbox that generates all kind of keys! 64-bit 128-bit 256-bit 512-bit 1024-bit 2048-bit 4096-bit. As the PyCrypto block-level encryption API is very low level, it only accepts 16-, 24-, or 32-bytes-long keys for AES-128, AES-196, and AES-256, respectively. Also, for AES encryption using pycrypto, you need to ensure that the data is a multiple of 16 bytes in length. Pad the buffer if it is not and include the size of the data at the. We use AES in a mode of operation in order to encrypt. The solutions above suggest using CBC, which is one example. Another is called CTR, and it’s somewhat easier to use: # AES supports multiple key sizes: 16 (AES128), 24 (AES192), or 32 (AES256). # pair (iv, ciphtertext). 'iv' stands for initialization vector. I was expecting AES code to be simpler to write than DES’ because AES was designed to be implemented in hardware or software, while DES design was geared towards hardware. This time, however, I decided to write an object-oriented API supporting the three different key sizes AES inherited from Rijndael (128-, 192- and 256-bit).

If you want encryption in Python, you may be interested in these libraries:

I spent a little bit of time last night and this morning trying to find someexamples for AES encryption using Python and PyCrypto. To my surprise, I had quite adifficult time finding an example of how to do it! I posted a message onTwitter asking for any solid examples, but people mostly just responded withthings I had seen before--the libraries that do the encryption, not examplesfor how to use the libraries.

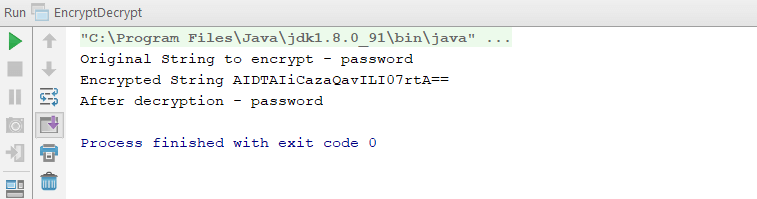
It wasn't long after that when I just decided to tackle the problem myself. Mysolution ended up being pretty simple (which is probably why there weren't anysolid examples for me to find). However, out of respect for those out therewho might still be looking for a solid example, here is my solution:

Edit: thanks to John and Kaso for their suggestions, though John's didn'tseem to work for me (?)

Edit 2015.12.14: thanks to Stephen for pointing out that the block size for AES is always 16, and the key size can be 16, 24, or 32. See FIPS-197 for more details.

If you plan to use this script, you'll need to have PyCrypto installed on yourcomputer. I have had a difficult time finding this for Windows in the past, soI will mirror the installer that I found overhere:http://jintoreedwine.wordpress.com/2008/07/20/python-25-and-encryption-pycrypto-under-windows/.I haven't tried it on Mac OS X yet, but it should be fairly simple to installit. Same goes for Linux.

Generate Aes 256 Key Python 3.5

The output of the script should always change with each execution thanks to therandom secret key. Here's some sample output:

If the comments in the script aren't explanatory enough, please comment and askfor clarification. I will offer any that I am capable of, and I invite othersto do the same.

In this section we shall explain how to implement elliptic-curve based public-key encryption / decryption (asymmetric encryption scheme based on ECC). This is non-trivial and usually involves a design of hybrid encryption scheme, involving ECC cryptography, ECDH key exchange and symmetric encryption algorithm.

Assume we have a ECC private-public key pair. We want to encrypt and decrypt data using these keys. By definition, asymmetric encryption works as follows: if we encrypt data by a private key, we will be able to decrypt the ciphertext later by the corresponding public key:

The above process can be directly applied for the RSA cryptosystem, but not for the ECC. The elliptic curve cryptography (ECC) does not directly provide encryption method. Instead, we can design a hybrid encryption scheme by using the ECDH (Elliptic Curve Diffie–Hellman) key exchange scheme to derive a shared secret key for symmetric data encryption and decryption.

This is how most hybrid encryption schemes works (the encryption process):

This is how most hybrid encryption schemes works (the decryption process):

Let's get into details how to design and implement an ECC-based hybrid encryption scheme.

ECC-Based Secret Key Derivation (using ECDH)

Assume we have a cryptographic elliptic curve over finite field, along with its generator point G. We can use the following two functions to calculate a shared a secret key for encryption and decryption (derived from the ECDH scheme):

• calculateEncryptionKey(pubKey) --> (sharedECCKey, ciphertextPubKey)
  1. Generate ciphertextPrivKey = new random private key.
  2. Calculate ciphertextPubKey = ciphertextPrivKey * G.
  3. Calculate the ECDH shared secret: sharedECCKey = pubKey * ciphertextPrivKey.
  4. Return both the sharedECCKey + ciphertextPubKey. Use the sharedECCKey for symmetric encryption. Use the randomly generated ciphertextPubKey to calculate the decryption key later.
• calculateDecryptionKey(privKey, ciphertextPubKey) --> sharedECCKey
  1. Calculate the the ECDH shared secret: sharedECCKey = ciphertextPubKey * privKey.
  2. Return the sharedECCKey and use it for the decryption.

The above calculations use the same math, like the ECDH algorithm (see the previous section). Recall that EC points have the following property:

• (a * G) * b = (b * G) * a

Now, assume that a = privKey, a * G = pubKey, b = ciphertextPrivKey, b * G = ciphertextPubKey.

The above equation takes the following form:

• pubKey * ciphertextPrivKey = ciphertextPubKey * privKey = sharedECCKey

This is what exactly the above two functions calculate, directly following the ECDH key agreement scheme. In the hybrid encryption schemes the encapsulated ciphertextPubKey is also known as 'ephemeral key', because it is used temporary, to derive the symmetric encryption key, using the ECDH key agreement scheme.

Generate Aes 256 Key Python 3.7

ECC-Based Secret Key Derivation - Example in Python

The below Python code uses the tinyec library to generate a ECC private-public key pair for the message recipient (based on the brainpoolP256r1 curve) and then derive a secret shared key (for encryption) and ephemeral ciphertext public key (for ECDH) from the recipient's public key and later derive the same secret shared key (for decryption) from the recipient's private key and the generated earlier ephemeral ciphertext public key:

Run the above code example: https://repl.it/@nakov/ECC-based-secret-key-derivation-in-Python.

The code is pretty simple and demonstrates that we can generate a pair { secret key + ciphertext public key } from given EC public key and later we can recover the same secret key from the pair { ciphertext public key + private key }. The above code produces output like this:

It is clear from the above output that the encryption key (derived from the public key) and the decryption key (derived from the corresponding private key) are the same. This is due to the above discussed property of the ECC: pubKey * ciphertextPrivKey = ciphertextPubKey * privKey. These keys will be used for data encryption and decryption in an integrated encryption scheme. The above output will be different if you run the code (due to the randomness used to generate ciphertextPrivKey, but the encryption and decryption keys will always be the same (the ECDH shared secret).

The above demonstrated mechanism for generating a shared ephemeral secret key, based on a ECC key pair, is an example of KEM (key encapsulation mechanism), based on the ECC and ECDH.

ECC-Based Hybrid Encryption / Decryption - Example in Python

Once we have the secret key, we can use it for symmetric data encryption, using a symmetric encryption scheme like AES-GCM or ChaCha20-Poly1305. Let's implement a fully-functional asymmetric ECC encryption and decryption hybrid scheme. It will be based on the brainpoolP256r1 curve and the AES-256-GCM authenticated symmetric cipher.

We shall use the tinyec and pycryptodome Python libraries respectively for ECC calculations and for the AES cipher:

Let's examine this full ECC + AES hybrid encryption example:

Run the above code example: https://repl.it/@nakov/ECC-based-hybrid-encryption-decryption-in-Python.

The above example starts from generating an ECC public + private key pair for the message recipient: pubKey + privKey, using the tinyec library. These keys will be used to encrypt the message msg through the hybrid encryption scheme (asymmetric ECC + symmetric AES) and to decrypt is later back to its original form.

Next, we encryptmsg by using the pubKey and we obtain as a result the following set of output: { ciphertext, nonce, authTag, ciphertextPubKey }. The ciphertext is obtained by the symmetric AES-GCM encryption, along with the nonce (random AES initialization vector) and authTag (the MAC code of the encrypted text, obtained by the GCM block mode). Additionally, we obtain a randomly generated ephemeral public key ciphertextPubKey, which will be encapsulated in the encrypted message and will be used to recover the AES symmetric key during the decryption (using the ECDH key agreement scheme, as it was show before).

To decrypt the encrypted message, we use the data produced during the encryption { ciphertext, nonce, authTag, ciphertextPubKey }, along with the decryption privateKey. The result is the decrypted plaintext message. We use authenticated encryption (GCM block mode), so if the decryption key or some other parameter is incorrect, the decryption will fail with an exception.

Internally, the encrypt_ECC(msg, pubKey) function first generates an ephemeral ECC key-pair for the ciphertext and calculates the symmetric encryption shared ECC key sharedECCKey = ciphertextPrivKey * pubKey. This key is an EC point, so it is then transformed to 256-bit AES secret key (integer) though hashing the point's x and y coordinates. Finally, the AES-256-GCM cipher (from pycryptodome) encrypts the message by the 256-bit shared secret key secretKey and produces as outputciphertext + nonce + authTag.

Generate Aes 256 Key Python

The decrypt_ECC(encryptedMsg{ciphertext, nonce, authTag, ciphertextPubKey}, privKey) function internally first calculates the symmetric encryption shared ECC key sharedECCKey = privKey * ciphertextPubKey. It is an EC point, so it should be first transformed to 256-bit AES secret key though hashing the point's x and y coordinates. Then the AES-256-GCM cipher is used to decrypt the ciphertext + nonce + authTag by the 256-bit shared secret key secretKey. The produced output is the original plaintext message (or an exception in case of incorrect decryption key or unmatching authTag).

The output from the above code looks like this:

Generate Aes 256 Key Python 3

Enjoy the above example, play with it, try to understand how exactly it works, try to change the underlying ECC curve, try to change the symmetric encryption algorithm, try to decrypt the ciphertext with wrong private key.